COEFICIENTE DE CORRELACIÓN DE PEARSON: 2014

COEFICIENTE DE CORRELACIÓN DE PEARSON

Es una medida de la relación lineal entre dos variables aleatorias cuantitativas. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de medida de las variables.

De manera menos formal, podemos definir el coeficiente de correlación de Pearson como un índice que puede utilizarse para medir el grado de relación de dos variables siempre y cuando ambas sean cuantitativas.

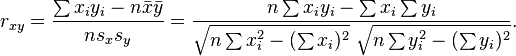
r_{xy}=\frac{\sum x_iy_i-n \bar{x} \bar{y}}{n s_x s_y}=\frac{n\sum x_iy_i-\sum x_i\sum y_i} {\sqrt{n\sum x_i^2-(\sum x_i)^2}~\sqrt{n\sum y_i^2-(\sum y_i)^2}}.

El fundamento del coeficiente de Pearson es el siguiente: Cuanto más intensa sea la concordancia (en sentido directo o inverso) de las posiciones relativas de los datos en las dos variables, el producto del numerador toma mayor valor (en sentido absoluto). Si la concordancia es exacta, el numerador es igual a N (o a -N), y el índice toma un valor igual a 1 (o -1).

Interpretación del coeficiente de Pearson

r = 1 Positiva perfecta

0.7 < r < 1 Positiva intensa

0.3 < r < 0.7 Positiva moderada

0.7 < r < 0.3 Positiva débil

r = 0.0 No hay relación lineal

- 0.3 < r < -0.0 Negativa debil

-0.7 < r < -0.3 Negariva moderada

-1 < r < -0.7 Negativa intensa

r = -1 Negativa perfecta

Características:

a) El coeficiente de correlación de Pearson puede tomar valores entre -1 y 1.

b) La correlación de una variable con ella misma siempre es igual a 1.

c) El valor 0 indica ausencia de covariación lineal, pero NO si la covariación es de tipo no lineal. (Ver ejemplo en el apartado de relaciones no lineales).

Recta de regresión por el método de los mínimos cuadrados

Cuando la nube de puntos adopta una forma definida, se pueden aproximar sus puntos mediante una línea curva en general, que llamamos curva de regresión.

Sólo nos ocuparemos del caso en el que la curva de regresión es una recta, llamada recta de regresión. Nos centraremos entonces en calcular la ecuación de una recta que "mejor se adapte" a una nube de puntos dada. En los ejemplos anteriores lo hemos hecho a ojo, ahora lo haremos con un criterio más preciso.

Para ello existen varios métodos, siendo el más utilizado el de los mínimos cuadrados. Consiste en hacer mínima la suma de los cuadrados de las diferencias entre los valores experimentales y los obtenidos mediante la recta. Por lo tanto, si consideramos la Y=aX+b, mediríamos lo bien (o mal) que se ajusta a nuestros puntos por medio de la cantidad

∑ i=1 N ( y i −( a x i +b ) ) 2 = ∑ i=1 N ( y i −a x i −b ) 2

y la recta que estamos buscando es la que haga esta cantidad lo más pequeña posible.

Una vez realizados los cálculos correspondientes, se tiene que la ecuación de la recta de regresión es:

y− y ¯ = σ xy σ x 2 (x− x ¯ )

donde σ_x σ_y son las desviaciones típicas de x e y.

Se comprueba que, como indicamos anteriormente, la recta obtenida pasa por el punto (x, y) que coincide con el centro de gravedad de la nube de puntos.

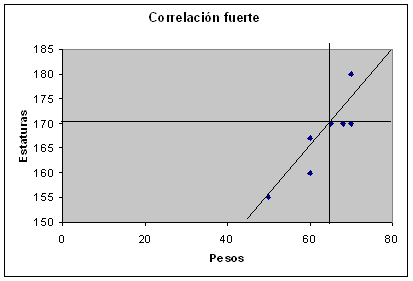
Ejemplo: Para el ejemplo de Pesos (kgs.) - Estaturas (cms.)

Peso en Kgs.	60	65	70	70	68	50	60
Altura en cms.	167	170	170	180	170	155	160
Frecuencias (n_i)	1	5	2	4	2	1	1

COEFICIENTE DE CORRELACIÓN DE PEARSON

martes, 18 de noviembre de 2014